Carvallo-Whipple Bicycle Model¶
Note
You can download this example as a Python script:
carvallo-whipple.py or Jupyter notebook:
carvallo-whipple.ipynb.
This example creates a nonlinear model and simulation of the Carvallo-Whipple Bicycle Model ([Carvallo1899], [Whipple1899]). This formulation uses the conventions described in [Moore2012] which are equivalent to the models described in [Meijaard2007] and [Basu-Mandal2007].
Import the necessary libraries, classes, and functions:
import numpy as np
from scipy.optimize import fsolve
import sympy as sm
import sympy.physics.mechanics as mec
from pydy.system import System
from pydy.viz import Sphere, Cylinder, VisualizationFrame, Scene
System Diagrams¶

Geometric variable definitions.¶
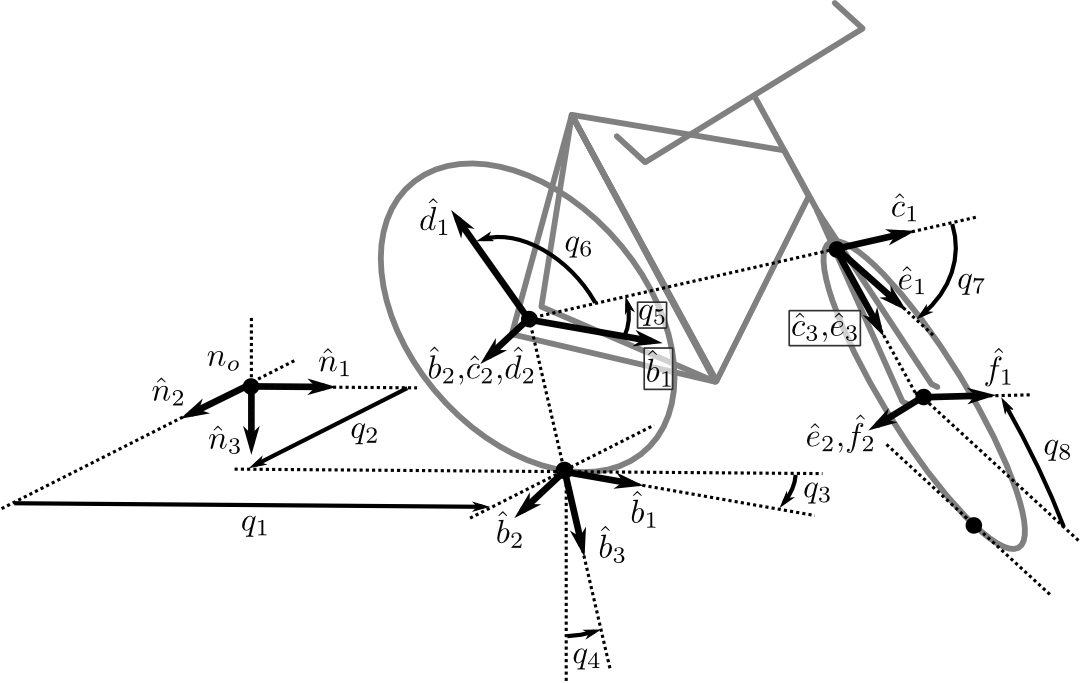
Configuration coordinate definitions.¶
Reference Frames¶
Use a reference frame that mimics the notation in [Moore2012].
class ReferenceFrame(mec.ReferenceFrame):
"""Subclass that enforces the desired unit vector indice style."""
def __init__(self, *args, **kwargs):
kwargs.pop('indices', None)
kwargs.pop('latexs', None)
lab = args[0].lower()
tex = r'\hat{{{}}}_{}'
super(ReferenceFrame, self).__init__(*args,
indices=('1', '2', '3'),
latexs=(tex.format(lab, '1'),
tex.format(lab, '2'),
tex.format(lab, '3')),
**kwargs)
Define some useful references frames:
\(N\): Newtonian Frame
\(A\): Yaw Frame, auxiliary frame
\(B\): Roll Frame, axillary frame
\(C\): Rear Frame
\(D\): Rear Wheel Frame
\(E\): Front Frame
\(F\): Front Wheel Frame
N = ReferenceFrame('N')
A = ReferenceFrame('A')
B = ReferenceFrame('B')
C = ReferenceFrame('C')
D = ReferenceFrame('D')
E = ReferenceFrame('E')
F = ReferenceFrame('F')
Generalized Coordinates and Speeds¶
All of the following variables are a functions of time, \(t\).
\(q_1\): perpendicular distance from the \(\hat{n}_2\) axis to the rear contact point in the ground plane
\(q_2\): perpendicular distance from the \(\hat{n}_1\) axis to the rear contact point in the ground plane
\(q_3\): frame yaw angle
\(q_4\): frame roll angle
\(q_5\): frame pitch angle
\(q_6\): front wheel rotation angle
\(q_7\): steering rotation angle
\(q_8\): rear wheel rotation angle
\(q_9\): perpendicular distance from the \(\hat{n}_2\) axis to the front contact point in the ground plane
\(q_{10}\): perpendicular distance from the \(\hat{n}_1\) axis to the front contact point in the ground plane
q1, q2, q3, q4 = mec.dynamicsymbols('q1 q2 q3 q4')
q5, q6, q7, q8 = mec.dynamicsymbols('q5 q6 q7 q8')
u1, u2, u3, u4 = mec.dynamicsymbols('u1 u2 u3 u4')
u5, u6, u7, u8 = mec.dynamicsymbols('u5 u6 u7 u8')
Orientation of Reference Frames¶
Declare the orientation of each frame to define the yaw, roll, and pitch of the rear frame relative to the Newtonian frame. The define steer of the front frame relative to the rear frame.
# rear frame yaw
A.orient(N, 'Axis', (q3, N['3']))
# rear frame roll
B.orient(A, 'Axis', (q4, A['1']))
# rear frame pitch
C.orient(B, 'Axis', (q5, B['2']))
# front frame steer
E.orient(C, 'Axis', (q7, C['3']))
Constants¶
Declare variables that are constant with respect to time for the model’s physical parameters.
\(r_f\): radius of front wheel
\(r_r\): radius of rear wheel
\(d_1\): the perpendicular distance from the steer axis to the center of the rear wheel (rear offset)
\(d_2\): the distance between wheels along the steer axis
\(d_3\): the perpendicular distance from the steer axis to the center of the front wheel (fork offset)
\(l_1\): the distance in the \(\hat{c}_1\) direction from the center of the rear wheel to the frame center of mass
\(l_2\): the distance in the \(\hat{c}_3\) direction from the center of the rear wheel to the frame center of mass
\(l_3\): the distance in the \(\hat{e}_1\) direction from the front wheel center to the center of mass of the fork
\(l_4\): the distance in the \(\hat{e}_3\) direction from the front wheel center to the center of mass of the fork
rf, rr = sm.symbols('rf rr')
d1, d2, d3 = sm.symbols('d1 d2 d3')
l1, l2, l3, l4 = sm.symbols('l1 l2 l3 l4')
# acceleration due to gravity
g = sm.symbols('g')
# mass
mc, md, me, mf = sm.symbols('mc md me mf')
# inertia
ic11, ic22, ic33, ic31 = sm.symbols('ic11 ic22 ic33 ic31')
id11, id22 = sm.symbols('id11 id22')
ie11, ie22, ie33, ie31 = sm.symbols('ie11 ie22 ie33 ie31')
if11, if22 = sm.symbols('if11 if22')
Specified¶
Declare three specified torques that are functions of time.
\(T_4\) : roll torque, between Newtonian frame and rear frame
\(T_6\) : rear wheel torque, between rear wheel and rear frame
\(T_7\) : steer torque, between rear frame and front frame
T4, T6, T7 = mec.dynamicsymbols('T4 T6 T7')
Position Vectors¶
# rear wheel contact point
dn = mec.Point('dn')
# rear wheel contact point to rear wheel center
do = mec.Point('do')
do.set_pos(dn, -rr * B['3'])
# rear wheel center to bicycle frame center
co = mec.Point('co')
co.set_pos(do, l1 * C['1'] + l2 * C['3'])
# rear wheel center to steer axis point
ce = mec.Point('ce')
ce.set_pos(do, d1 * C['1'])
# steer axis point to the front wheel center
fo = mec.Point('fo')
fo.set_pos(ce, d2 * E['3'] + d3 * E['1'])
# front wheel center to front frame center
eo = mec.Point('eo')
eo.set_pos(fo, l3 * E['1'] + l4 * E['3'])
# locate the point fixed on the wheel which instantaneously touches the
# ground
fn = mec.Point('fn')
fn.set_pos(fo, rf * E['2'].cross(A['3']).cross(E['2']).normalize())
Holonomic Constraint¶
The front contact point \(f_n\) and the rear contact point \(d_n\) must both reside in the ground plane.
holonomic = fn.pos_from(dn).dot(A['3'])
This expression defines a configuration constraint among \(q_4\), \(q_5\), and \(q_7\).
mec.find_dynamicsymbols(holonomic)
{q4(t), q5(t), q7(t)}
Kinematical Differential Equations¶
Define the generalized speeds all as \(u=\dot{q}\).
t = mec.dynamicsymbols._t
kinematical = [q3.diff(t) - u3, # yaw
q4.diff(t) - u4, # roll
q5.diff(t) - u5, # pitch
q7.diff(t) - u7] # steer
Angular Velocities¶
A.set_ang_vel(N, u3 * N['3']) # yaw rate
B.set_ang_vel(A, u4 * A['1']) # roll rate
C.set_ang_vel(B, u5 * B['2']) # pitch rate
D.set_ang_vel(C, u6 * C['2']) # rear wheel rate
E.set_ang_vel(C, u7 * C['3']) # steer rate
F.set_ang_vel(E, u8 * E['2']) # front wheel rate
Linear Velocities¶
# rear wheel contact stays in ground plane and does not slip
dn.set_vel(N, 0.0 * N['1'])
# mass centers
do.v2pt_theory(dn, N, D)
co.v2pt_theory(do, N, C)
ce.v2pt_theory(do, N, C)
fo.v2pt_theory(ce, N, E)
eo.v2pt_theory(fo, N, E)
# wheel contact velocities
fn.v2pt_theory(fo, N, F); # supress output
Motion Constraints¶
Enforce the no slip condition at the front wheel contact point. Note that the
no-slip condition is already enforced with the velocity of \(n_o\) set to
0. Also include an extra motion constraint not allowing vertical motion of the
contact point. Note that this is an integrable constraint, i.e. the derivative
of nonholonomic above. It is not a nonholonomic constraint, but we include
it because we can’t easy eliminate a dependent generalized coordinate with
nonholonmic.
Warning
The floating point numerical stability of the solution is affected
by the order of the nonholonomic constraint expressions in the following
list. If ordered A['1'],A['2'],A['3'] stability degrades.
nonholonomic = [
fn.vel(N).dot(A['1']),
fn.vel(N).dot(A['3']),
fn.vel(N).dot(A['2']),
]
Inertia¶
The inertia dyadics are defined with respect to the rear and front frames.
Ic = mec.inertia(C, ic11, ic22, ic33, 0.0, 0.0, ic31)
Id = mec.inertia(C, id11, id22, id11, 0.0, 0.0, 0.0)
Ie = mec.inertia(E, ie11, ie22, ie33, 0.0, 0.0, ie31)
If = mec.inertia(E, if11, if22, if11, 0.0, 0.0, 0.0)
Rigid Bodies¶
rear_frame = mec.RigidBody('Rear Frame', co, C, mc, (Ic, co))
rear_wheel = mec.RigidBody('Rear Wheel', do, D, md, (Id, do))
front_frame = mec.RigidBody('Front Frame', eo, E, me, (Ie, eo))
front_wheel = mec.RigidBody('Front Wheel', fo, F, mf, (If, fo))
bodies = [rear_frame, rear_wheel, front_frame, front_wheel]
Loads¶
# gravity
Fco = (co, mc*g*A['3'])
Fdo = (do, md*g*A['3'])
Feo = (eo, me*g*A['3'])
Ffo = (fo, mf*g*A['3'])
# input torques
Tc = (C, T4*A['1'] - T6*B['2'] - T7*C['3'])
Td = (D, T6*C['2'])
Te = (E, T7*C['3'])
loads = [Fco, Fdo, Feo, Ffo, Tc, Td, Te]
Kane’s Method¶
kane = mec.KanesMethod(N,
[q3, q4, q7], # yaw, roll, steer
[u4, u6, u7], # roll rate, rear wheel rate, steer rate
kd_eqs=kinematical,
q_dependent=[q5], # pitch angle
configuration_constraints=[holonomic],
u_dependent=[u3, u5, u8], # yaw rate, pitch rate, front wheel rate
velocity_constraints=nonholonomic)
fr, frstar = kane.kanes_equations(bodies, loads)
Simulating the system¶
PyDy’s System is a wrapper that holds the KanesMethod object to
integrate the equations of motion using numerical values of constants.
from pydy.system import System
sys = System(kane)
Now, we specify the numerical values of the constants and the initial values of states in the form of a dict. The are the benchmark values used in [Meijaard2007] converted to the [Moore2012] formulation.
sys.constants = {
rf: 0.35,
rr: 0.3,
d1: 0.9534570696121849,
d3: 0.03207142672761929,
d2: 0.2676445084476887,
l1: 0.4707271515135145,
l2: -0.47792881146460797,
l4: -0.3699518200282974,
l3: -0.00597083392418685,
mc: 85.0,
md: 2.0,
me: 4.0,
mf: 3.0,
id11: 0.0603,
id22: 0.12,
if11: 0.1405,
if22: 0.28,
ic11: 7.178169776497895,
ic22: 11.0,
ic31: 3.8225535938357873,
ic33: 4.821830223502103,
ie11: 0.05841337700152972,
ie22: 0.06,
ie31: 0.009119225261946298,
ie33: 0.007586622998470264,
g: 9.81
}
Setup the initial conditions such that the bicycle is traveling at some forward speeds and has an initial positive roll rate.
initial_speed = 4.6 # m/s
initial_roll_rate = 0.5 # rad/s
The initial configuration will be the upright equilibrium position. The holonomic constraint requires that either the roll, pitch, or steer angle need be dependent. Below, the pitch angle is taken as dependent and solved for using fsolve(). Note that it is equivalent to the steer axis tilt [Meijaard2007].
eval_holonomic = sm.lambdify((q5, q4, q7, d1, d2, d3, rf, rr), holonomic)
initial_pitch_angle = float(fsolve(eval_holonomic, 0.0,
args=(0.0, # q4
1e-8, # q7
sys.constants[d1],
sys.constants[d2],
sys.constants[d3],
sys.constants[rf],
sys.constants[rr])))
np.rad2deg(initial_pitch_angle)
18.000000000000007
Set all of the initial conditions.
Warning
A divide-by-zero will occur if the steer angle is set to zero. Thus the 1e-8 values. The integration is also sensitive to the size of this value. This shouldn’t be the case and may point to some errors in the derivation and implementation. More careful attention to the integration tolerances may help too.
sys.initial_conditions = {q3: 0.0,
q4: 0.0,
q5: initial_pitch_angle,
q7: 1e-8,
u3: 0.0,
u4: initial_roll_rate,
u5: 0.0,
u6: -initial_speed/sys.constants[rr],
u7: 0.0,
u8: -initial_speed/sys.constants[rf]}
Generate a time vector over which the integration will be carried out.
fps = 30 # frames per second
duration = 6.0 # seconds
sys.times = np.linspace(0.0, duration, num=int(duration*fps))
The trajectory of the states over time can be found by calling the
.integrate() method. But due to the complexity of the equations of motion
it is helpful to use the cython generator for faster numerical evaluation.
Warning
The holonomic constraint equation is not explicitly enforced, as PyDy does not yet support integration of differential algebraic equations (DAEs) yet. The solution will drift from the true solution over time with magnitudes dependent on the intiial conditions and constants values.
sys.generate_ode_function(generator='cython')
x_trajectory = sys.integrate()
Evaluate the holonomic constraint across the simulation.
holonomic_vs_time = eval_holonomic(x_trajectory[:, 3], # q5
x_trajectory[:, 1], # q4
x_trajectory[:, 2], # q7
sys.constants[d1],
sys.constants[d2],
sys.constants[d3],
sys.constants[rf],
sys.constants[rr])
Plot the State Trajectories¶
import matplotlib.pyplot as plt
fig, axes = plt.subplots(len(sys.states) + 1, 1, sharex=True)
fig.set_size_inches(8, 10)
for ax, traj, s in zip(axes, x_trajectory.T, sys.states):
ax.plot(sys.times, traj)
ax.set_ylabel(s)
axes[-1].plot(sys.times, np.squeeze(holonomic_vs_time))
axes[-1].set_ylabel('Holonomic\nconstraint [m]')
axes[-1].set_xlabel('Time [s]')
plt.tight_layout()
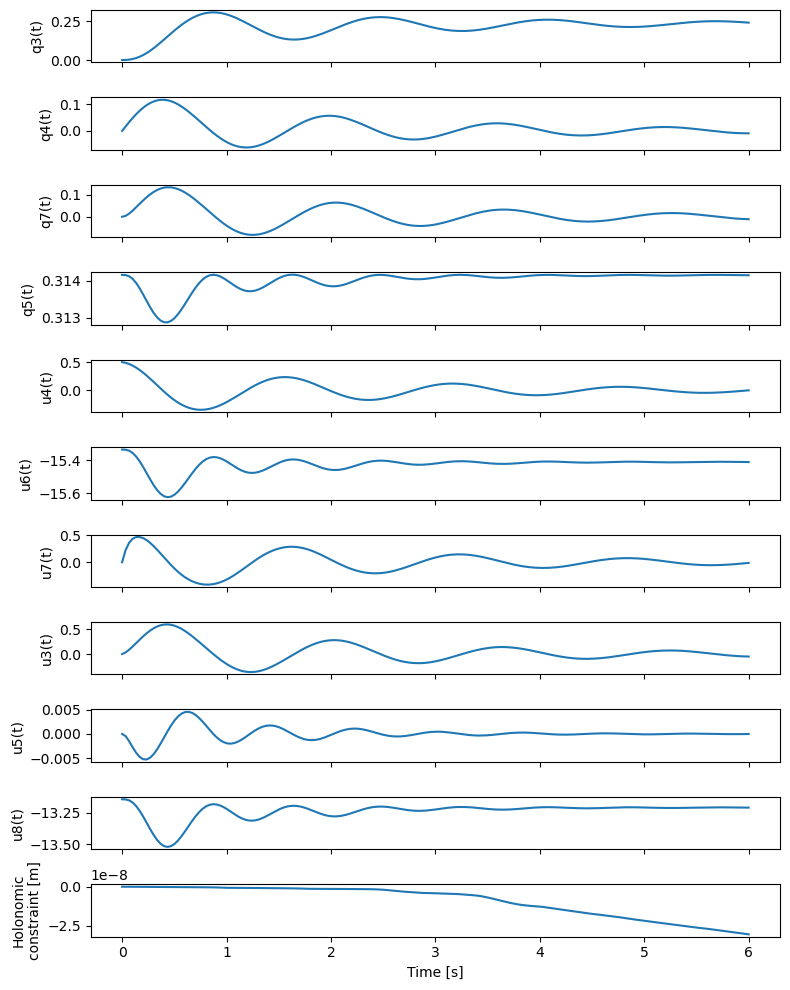
Visualizing the System Motion¶
Create two cylinders to represent the front and rear wheels.
rear_wheel_circle = Cylinder(radius=sys.constants[rr], length=0.01,
color="green", name='rear wheel')
front_wheel_circle = Cylinder(radius=sys.constants[rf], length=0.01,
color="green", name='front wheel')
rear_wheel_vframe = VisualizationFrame(B, do, rear_wheel_circle)
front_wheel_vframe = VisualizationFrame(E, fo, front_wheel_circle)
Create some cylinders to represent the front and rear frames.
d1_cylinder = Cylinder(radius=0.02, length=sys.constants[d1],
color='black', name='rear frame d1')
d2_cylinder = Cylinder(radius=0.02, length=sys.constants[d2],
color='black', name='front frame d2')
d3_cylinder = Cylinder(radius=0.02, length=sys.constants[d3],
color='black', name='front frame d3')
d1_frame = VisualizationFrame(C.orientnew('C_r', 'Axis', (sm.pi/2, C.z)),
do.locatenew('d1_half', d1/2*C.x), d1_cylinder)
d2_frame = VisualizationFrame(E.orientnew('E_r', 'Axis', (-sm.pi/2, E.x)),
fo.locatenew('d2_half', -d3*E.x - d2/2*E.z), d2_cylinder)
d3_frame = VisualizationFrame(E.orientnew('E_r', 'Axis', (sm.pi/2, E.z)),
fo.locatenew('d3_half', -d3/2*E.x), d3_cylinder)
Create some spheres to represent the mass centers of the front and rear frames.
co_sphere = Sphere(radius=0.05, color='blue', name='rear frame co')
eo_sphere = Sphere(radius=0.05, color='blue', name='rear frame eo')
co_frame = VisualizationFrame(C, co, co_sphere)
eo_frame = VisualizationFrame(E, eo, eo_sphere)
Create the scene and add the visualization frames.
scene = Scene(N, dn, system=sys)
scene.visualization_frames = [front_wheel_vframe, rear_wheel_vframe,
d1_frame, d2_frame, d3_frame,
co_frame, eo_frame]
Now, call the display method.
scene.display_jupyter(axes_arrow_length=5.0)
References¶
- Whipple1899
Whipple, Francis J. W. “The Stability of the Motion of a Bicycle.” Quarterly Journal of Pure and Applied Mathematics 30 (1899): 312–48.
- Carvallo1899
Carvallo, E. Théorie Du Mouvement Du Monocycle et de La Bicyclette. Paris, France: Gauthier- Villars, 1899.
- Moore2012(1,2,3)
Moore, Jason K. “Human Control of a Bicycle.” Doctor of Philosophy, University of California, 2012. http://moorepants.github.io/dissertation.
- Meijaard2007(1,2,3)
Meijaard, J. P., Jim M. Papadopoulos, Andy Ruina, and A. L. Schwab. “Linearized Dynamics Equations for the Balance and Steer of a Bicycle: A Benchmark and Review.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 463, no. 2084 (August 8, 2007): 1955–82.
- Basu-Mandal2007
Basu-Mandal, Pradipta, Anindya Chatterjee, and J.M Papadopoulos. “Hands-Free Circular Motions of a Benchmark Bicycle.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 463, no. 2084 (August 8, 2007): 1983–2003. https://doi.org/10.1098/rspa.2007.1849.