Modeling of a Variable-Mass Nonholonomic Gyrostatic Rocket Car Using Extended Kane’s Equations

Note

You can download this example as a Python script: rocket-car.py or Jupyter notebook: rocket-car.ipynb.

This is an implementation of the nonholonomic rocket-engine-powered jet racing car example from [Ge1982]. This example provides insight into analytically modeling variable-mass systems using Kane’s method and the extended Kane’s equations for variable-mass systems. It also demonstrates the efficacy of Kane’s method in the modeling of complex dynamical systems.

../_images/rocket-car.svg

An idealized model of a jet racing car that is propelled by a rocket engine at point P is considered. The rocket engine is treated as a variable-mass particle at P.

Here, \(\{a_x: g_3, a_y: g_1, a_z: g_2\}\)

import sympy as sm
import sympy.physics.mechanics as me
from pydy.system import System
import numpy as np
from sympy.simplify.fu import TR2
import matplotlib.pyplot as plt
from scipy.integrate import odeint
me.init_vprinting()

from IPython.display import Latex, display
def print_answer(x, x_res):
    for xi, xri in zip(x, x_res):
        display(Latex(sm.latex(sm.Eq(xi, xri), mode='inline')))

Reference Frames, Generalized Coordinates, and Generalized Speeds

N = me.ReferenceFrame('N')

q1, q2, q3, q4, q5, q6, q7, q8 = me.dynamicsymbols('q1:9')

A2 = N.orientnew('A_2', 'Axis', [q3, N.z])
A1 = A2.orientnew('A_1', 'Axis', [q4, A2.z])

B1 = A1.orientnew('B_1', 'Axis', [q5, A1.y])
B2 = A1.orientnew('B_2', 'Axis', [q6, A1.y])
B3 = A2.orientnew('B_3', 'Axis', [q7, A2.y])
B4 = A2.orientnew('B_4', 'Axis', [q8, A2.y])

t = me.dynamicsymbols._t

O = me.Point('O') # fixed point in the inertial reference frame
O.set_vel(N, 0)

L, l , a, b, r1, r2 = sm.symbols('L, l , a, b, r_1, r_2')

Q = O.locatenew('Q', q1 * N.x + q2 * N.y)

P = Q.locatenew('P', L * -A2.x)

C = P.locatenew('C', l * A2.x)

Q.set_vel(N, Q.pos_from(O).dt(N))
Q.vel(N)
../_images/rocket-car_7_0.png 
P.v2pt_theory(Q, N, A2)
P.vel(N)
../_images/rocket-car_8_0.png 
C.v2pt_theory(P, N, A2)
# C.vel(N)
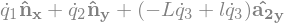
../_images/rocket-car_9_0.png 
A1.ang_vel_in(A2).express(A1)
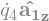
../_images/rocket-car_10_0.png 
u1, u2 = me.dynamicsymbols('u_1:3')

z1 = sm.Eq(u1, A1.ang_vel_in(A2).dot(A1.z))
z2 = sm.Eq(u2, Q.vel(N).dot(A1.x))

u = sm.trigsimp(sm.solve([z1, z2], A1.ang_vel_in(A2).dot(A1.z), Q.vel(N).dot(A1.x)))
u
../_images/rocket-car_13_0.png

Formulation of the Constraint Equations

Nonholonomic Constraints: \(B_1\)

B1_center = Q.locatenew('B_1_center', a * A1.y)
B1_center.pos_from(Q)
../_images/rocket-car_14_0.png 
B1_center.v2pt_theory(Q, N, A1)
B1_center.vel(N).express(A1).simplify()
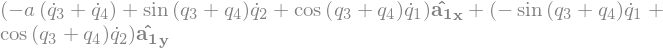
../_images/rocket-car_15_0.png 
B1_ground = B1_center.locatenew('B_1_ground', r1 * -A1.z)
B1_ground.pos_from(B1_center)
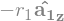
../_images/rocket-car_16_0.png 
B1_ground.v2pt_theory(B1_center, N, B1)
B1_ground.vel(N).simplify()
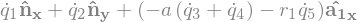
../_images/rocket-car_17_0.png 
B1_cons = [me.dot(B1_ground.vel(N).simplify(), uv) for uv in A1]
for i in range(len(B1_cons)):
    display(sm.trigsimp(B1_cons[i]))
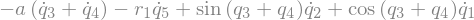
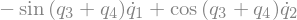
../_images/rocket-car_18_0.png ../_images/rocket-car_18_1.png ../_images/rocket-car_18_2.png 
eq1 = sm.Eq(B1_cons[0].simplify().subs(u), 0)
eq1
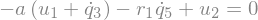
../_images/rocket-car_19_0.png 
eq2 = sm.Eq(B1_cons[1].simplify().subs(u), 0)
eq2
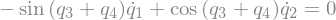
../_images/rocket-car_20_0.png

Nonholonomic Constraints: \(B_2\)

B2_center = Q.locatenew('B_1_center', a * -A1.y)
B2_center.pos_from(Q)
../_images/rocket-car_21_0.png 
B2_center.v2pt_theory(Q, N, A1)
B2_center.vel(N).express(A1).simplify()
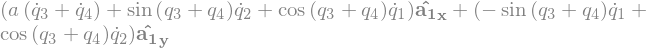
../_images/rocket-car_22_0.png 
B2_ground = B2_center.locatenew('B_2_ground', r1 * -A1.z)
B2_ground.pos_from(B2_center)
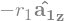
../_images/rocket-car_23_0.png 
B2_ground.v2pt_theory(B2_center, N, B2)
B2_ground.vel(N).simplify()
../_images/rocket-car_24_0.png 
B2_cons = [me.dot(B2_ground.vel(N).simplify(), uv) for uv in A1]
for i in range(len(B2_cons)):
    display(sm.trigsimp(B2_cons[i]))
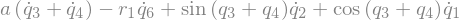
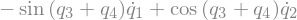
../_images/rocket-car_25_0.png ../_images/rocket-car_25_1.png ../_images/rocket-car_25_2.png 
eq3 = sm.Eq(B2_cons[0].simplify().subs(u), 0)
eq3
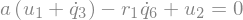
../_images/rocket-car_26_0.png 
eq4 = sm.Eq(B2_cons[1].simplify().subs(u), 0)
eq4
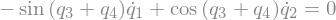
../_images/rocket-car_27_0.png

Nonholonomic Constraints: \(B_3\)

B3_center = P.locatenew('B_3_center', b * A2.y)
B3_center.pos_from(P)
../_images/rocket-car_28_0.png 
B3_center.v2pt_theory(P, N, A2)
B3_center.vel(N).express(A2).simplify()
../_images/rocket-car_29_0.png 
B3_ground = B3_center.locatenew('B_3_ground', r2 * -A2.z)
B3_ground.pos_from(B3_center)
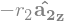
../_images/rocket-car_30_0.png 
B3_ground.v2pt_theory(B3_center, N, B3)
B3_ground.vel(N).simplify()
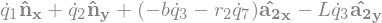
../_images/rocket-car_31_0.png 
B3_cons = [me.dot(B3_ground.vel(N).simplify(), uv) for uv in A2]
for i in range(len(B3_cons)):
    display(sm.trigsimp(B3_cons[i]))
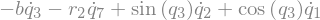
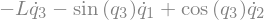
../_images/rocket-car_32_0.png ../_images/rocket-car_32_1.png ../_images/rocket-car_32_2.png 
eq5 = sm.Eq(B3_cons[0].simplify().subs(u), 0)
eq5
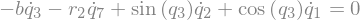
../_images/rocket-car_33_0.png 
eq6 = sm.Eq(B3_cons[1].simplify().subs(u), 0)
eq6
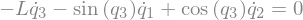
../_images/rocket-car_34_0.png

Nonholonomic Constraints: \(B_4\)

B4_center = P.locatenew('B_4_center', b * -A2.y)
B4_center.pos_from(P)
../_images/rocket-car_35_0.png 
B4_center.v2pt_theory(P, N, A2)
B4_center.vel(N).express(A2).simplify()
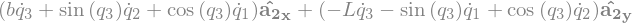
../_images/rocket-car_36_0.png 
B4_ground = B4_center.locatenew('B_4_ground', r2 * -A2.z)
B4_ground.pos_from(B4_center)
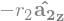
../_images/rocket-car_37_0.png 
B4_ground.v2pt_theory(B4_center, N, B4)
B4_ground.vel(N).simplify()
../_images/rocket-car_38_0.png 
B4_cons = [me.dot(B4_ground.vel(N).simplify(), uv) for uv in A2]
for i in range(len(B4_cons)):
    display(sm.trigsimp(B4_cons[i]))
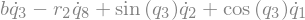
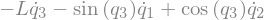
../_images/rocket-car_39_0.png ../_images/rocket-car_39_1.png ../_images/rocket-car_39_2.png 
eq7 = sm.Eq(B4_cons[0].simplify().subs(u), 0)
eq7
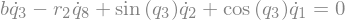
../_images/rocket-car_40_0.png 
eq8 = sm.Eq(B4_cons[1].simplify().subs(u), 0)
eq8
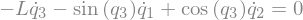
../_images/rocket-car_41_0.png

\(\text{LHS} \Longleftrightarrow \text{RHS}\ \text{in}\ z_1, z_2 \rightarrow \text{Equations}\ 9, 10\)

eq9 = sm.Eq(A1.ang_vel_in(A2).dot(A1.z), u1)
eq9
../_images/rocket-car_42_0.png 
eq10 = sm.Eq(Q.vel(N).dot(A1.x), u2)
eq10
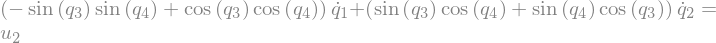
../_images/rocket-car_43_0.png

Solving the System of Linear Equations

The system of equations is linear in \(\dot{q}_1, \dot{q}_2,...\)

Note: eq4 \(\equiv\) eq2; eq8 \(\equiv\) eq6

solution = sm.linsolve([eq1, eq2, eq3, eq5, eq6, eq7, eq9, eq10], q1.diff(), q2.diff(), q3.diff(),  q4.diff(), q5.diff(), q6.diff(), q7.diff(), q8.diff())

sollist_keys = [q1.diff(), q2.diff(), q3.diff(),  q4.diff(), q5.diff(), q6.diff(), q7.diff(), q8.diff()]
sollist_keys
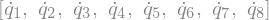
../_images/rocket-car_45_0.png 
sollist_values = list(solution.args[0])

sollist_values_simple = []
for i in range(len(sollist_values)):
    sollist_values_simple.append(sm.factor(TR2(sollist_values[i]).simplify()))

soldict = dict(zip(sollist_keys, sollist_values_simple))
print_answer(sollist_keys, sollist_values_simple)
\[\frac{d}{d t} q_{1}{\left(t \right)} = u_{2}{\left(t \right)} \cos{\left(q_{3}{\left(t \right)} + q_{4}{\left(t \right)} \right)}\]
\[\frac{d}{d t} q_{2}{\left(t \right)} = u_{2}{\left(t \right)} \sin{\left(q_{3}{\left(t \right)} + q_{4}{\left(t \right)} \right)}\]
\[\frac{d}{d t} q_{3}{\left(t \right)} = u_{2}{\left(t \right)} \sin{\left(q_{4}{\left(t \right)} \right)} / L\]
\[\frac{d}{d t} q_{4}{\left(t \right)} = u_{1}{\left(t \right)}\]
\[\frac{d}{d t} q_{5}{\left(t \right)} = - \left(L a u_{1}{\left(t \right)} - L u_{2}{\left(t \right)} + a u_{2}{\left(t \right)} \sin{\left(q_{4}{\left(t \right)} \right)}\right) / L r_{1}\]
\[\frac{d}{d t} q_{6}{\left(t \right)} = \left(L a u_{1}{\left(t \right)} + L u_{2}{\left(t \right)} + a u_{2}{\left(t \right)} \sin{\left(q_{4}{\left(t \right)} \right)}\right) / L r_{1}\]
\[\frac{d}{d t} q_{7}{\left(t \right)} = - \left(- L \cos{\left(q_{4}{\left(t \right)} \right)} + b \sin{\left(q_{4}{\left(t \right)} \right)}\right) u_{2}{\left(t \right)} / L r_{2}\]
\[\frac{d}{d t} q_{8}{\left(t \right)} = \left(L \cos{\left(q_{4}{\left(t \right)} \right)} + b \sin{\left(q_{4}{\left(t \right)} \right)}\right) u_{2}{\left(t \right)} / L r_{2}\]

Reformulated Velocity and Angular Velocity Expressions

N_v_Q = Q.vel(N).subs(soldict).express(A1).simplify()
N_v_Q
../_images/rocket-car_49_0.png 
N_v_P = P.vel(N).subs(soldict).express(A2).simplify()
N_v_P
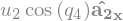
../_images/rocket-car_50_0.png 
N_v_C = C.vel(N).subs(soldict).express(A2).simplify()
N_v_C
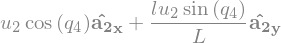
../_images/rocket-car_51_0.png 
N_w_A1 = A1.ang_vel_in(N).subs(soldict).express(A1).simplify()
N_w_A1
../_images/rocket-car_52_0.png 
N_w_A2 = A2.ang_vel_in(N).subs(soldict).express(A2).simplify()
N_w_A2
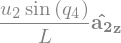
../_images/rocket-car_53_0.png

Partial Velocities and Partial Angular Velocities

V_1_Q = N_v_Q.diff(u1, N)
V_1_Q
../_images/rocket-car_54_0.png 
V_2_Q = N_v_Q.diff(u2, N)
V_2_Q
../_images/rocket-car_55_0.png 
V_1_C = N_v_C.diff(u1, N)
V_1_C
../_images/rocket-car_56_0.png 
V_2_C = N_v_C.diff(u2, N)
V_2_C
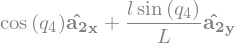
../_images/rocket-car_57_0.png 
V_1_P = N_v_P.diff(u1, N)
V_1_P
../_images/rocket-car_58_0.png 
V_2_P = N_v_P.diff(u2, N)
V_2_P
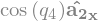
../_images/rocket-car_59_0.png 
w_1_A1 = N_w_A1.diff(u1, N)
w_1_A1
../_images/rocket-car_60_0.png 
w_2_A1 = N_w_A1.diff(u2, N)
w_2_A1
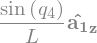
../_images/rocket-car_61_0.png 
w_1_A2 = N_w_A2.diff(u1, N)
w_1_A2
../_images/rocket-car_62_0.png 
w_2_A2 = N_w_A2.diff(u2, N)
w_2_A2
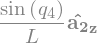
../_images/rocket-car_63_0.png

Accelerations and Angular Accelerations

a_1__P, a_2__P, a_3__P, a_1__C, a_2__C, a_3__C, a__Q, alpha__A1, alpha__A2 = sm.symbols('a_1__P, a_2__P, a_3__P, a_1__C, a_2__C, a_3__C, a__Q, alpha__A1, alpha__A2')

N_a_P = N_v_P.dt(N).subs(soldict)
N_a_P
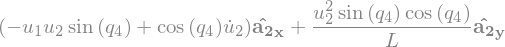
../_images/rocket-car_65_0.png 
N_a_C = N_v_C.dt(N).subs(soldict)
N_a_C
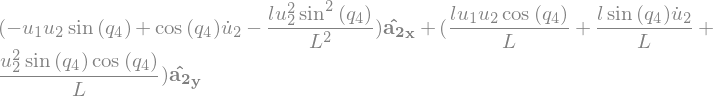
../_images/rocket-car_66_0.png 
N_a_Q = N_v_Q.dt(N).subs(soldict)
N_a_Q
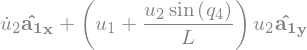
../_images/rocket-car_67_0.png 
N_aa_A1 = N_w_A1.dt(N).subs(soldict)
N_aa_A1
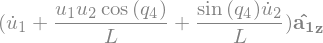
../_images/rocket-car_68_0.png 
N_aa_A2 = N_w_A2.dt(N).subs(soldict)
N_aa_A2
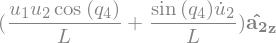
../_images/rocket-car_69_0.png

Forces and Torques

\((F_r^*)_G = (F_r^*)_{GR} + (F_r^*)_{GI}\)

where,

\((F_r^*)_{GR} = {V_r}^G \cdot {F_G}^* + \omega_r^A \cdot {T_G}^*\)

\(F_G^* = -m_G {a^G}^*\)

\(T_G^* \overset{\Delta}{=} -[\alpha_A \cdot I_G + \omega_r^A \times (I_G \cdot \omega_r^A)]\)

\(({F_r}^*)_{GI} = -J\{\omega_r^A [\ddot{q_k} g_1 + \dot{q_k} (\omega_3^A g_2 - \omega_2^A g_3)] + C_{kr} (\dot{\omega_1^A} + \ddot{q_k}) \}\)

[Kane1978]

Naming Convention:

\(({F_r}^*)_{G_n R}\) (rigid)

\(({F_r}^*)_{G_n I}\) (internal)

Masses and Moments of Inertia

M1, M2 = sm.symbols('M_1, M_2')
m = me.dynamicsymbols('m')

I1x, I1y, I1z = sm.symbols('I_{1_x}, I_{1_y}, I_{1_z}')
I2x, I2y, I2z = sm.symbols('I_{2_x}, I_{2_y}, I_{2_z}')
J1, J2 = sm.symbols('J_1, J_2')

I1 = me.inertia(A1, I1x, I1y, I1z)
I1
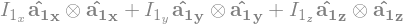
../_images/rocket-car_72_0.png 
I2 = me.inertia(A2, I2x, I2y, I2z)
I2
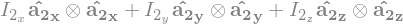
../_images/rocket-car_73_0.png

Gyrostat \(G_1\)

\(\rightarrow {F_G}^* = -m_G {a^G}^*\)

Fstar_G1 = -M1 * N_a_Q
Fstar_G1
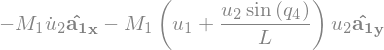
../_images/rocket-car_74_0.png

\(\rightarrow {T_G}^* \overset{\Delta}{=} -[\alpha_A \cdot I_G + {\omega_r}^A \times (I_G \cdot {\omega_r}^A)]\)

Tstar_G1 = -(N_aa_A1.dot(I1) + me.cross(N_w_A1, I1.dot(N_w_A1)))
Tstar_G1
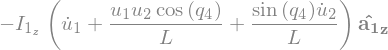
../_images/rocket-car_75_0.png

\(\rightarrow ({F_r}^*)_{GR} = {V_r}^G \cdot {F_G}^* + {\omega_r}^A \cdot {T_G}^*\)

Fstar_1_G1_R = V_1_Q.dot(Fstar_G1) + w_1_A1.dot(Tstar_G1).subs(soldict)
Fstar_1_G1_R.subs({N_w_A1.dt(N).subs(soldict).dot(A1.z): alpha__A1})
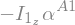
../_images/rocket-car_76_0.png 
Fstar_2_G1_R = V_2_Q.dot(Fstar_G1) + w_2_A1.dot(Tstar_G1).subs(soldict)
Fstar_2_G1_R.subs({N_w_A1.dt(N).subs(soldict).dot(A1.z): alpha__A1})
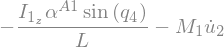
../_images/rocket-car_77_0.png

\(\rightarrow (F_r^*)_{GI} = -J\{\omega_r^A \cdot [\ddot{q_k} g_1 + \dot{q_k} (\omega_3^A g_2 - \omega_2^A g_3)] + C_{kr} (\dot{\omega}_1^A + \ddot{q_k}) \} \qquad (r=1,...,n-m)\)

Here, \(\{\omega_1^A: \omega_2^A,\ \omega_2^A: \omega_3^A,\ \omega_3^A: \omega_1^A\}\)

\(\rightarrow \dot{q_k} = \sum_{s = 1}^{n - m} C_{ks} u_s + D_k\) (Generalized Speeds)

\(\omega_i^A \overset{\Delta}{=} \omega^A \cdot \hat{g}_i \quad (i = 1, 2, 3)\)

# C_kr
C51, C61 = sm.symbols('C_51, C_61')
C_51 = soldict[q5.diff()].diff(u1)
C_61 = soldict[q6.diff()].diff(u1)
Fstar_1_G1_I = -J1 * (N_w_A1.dot(q5.diff().diff() * A1.y + q5.diff()*(N_w_A1.dot(A1.x)*A1.z - N_w_A1.dot(A1.z)*A1.x)) + C_51 * (N_w_A1.dot(A1.y).diff() + q5.diff().diff())) \
               -J1 * (N_w_A1.dot(q6.diff().diff() * A1.y + q6.diff()*(N_w_A1.dot(A1.x)*A1.z - N_w_A1.dot(A1.z)*A1.x)) + C_61 * (N_w_A1.dot(A1.y).diff() + q6.diff().diff()))   # B1 \ B2

Fstar_1_G1_I, C_51, C_61, Fstar_1_G1_I.subs({-C_51: -C51, -C_61: -C61}).simplify()
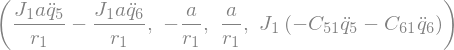
../_images/rocket-car_78_0.png 
# C_kr
C52, C62 = sm.symbols('C_52, C_62')
C_52 = soldict[q5.diff()].diff(u2)
C_62 = soldict[q6.diff()].diff(u2)
Fstar_2_G1_I = -J1 * (N_w_A1.dot(q5.diff().diff() * A1.y + q5.diff()*(N_w_A1.dot(A1.x)*A1.z - N_w_A1.dot(A1.z)*A1.x)) + C_52 * (N_w_A1.dot(A1.y).diff() + q5.diff().diff())) \
               -J1 * (N_w_A1.dot(q6.diff().diff() * A1.y + q6.diff()*(N_w_A1.dot(A1.x)*A1.z - N_w_A1.dot(A1.z)*A1.x)) + C_62 * (N_w_A1.dot(A1.y).diff() + q6.diff().diff()))   # B1 \ B2

display(Fstar_2_G1_I),
display(C_52)
display(C_62)
display(Fstar_2_G1_I.subs({-C_52: -C52, -C_62: -C62}).simplify())
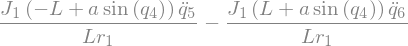
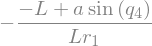
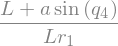
../_images/rocket-car_79_0.png ../_images/rocket-car_79_1.png ../_images/rocket-car_79_2.png ../_images/rocket-car_79_3.png

\(\rightarrow (F_r^*)_G = (F_r^*)_{GR} + (F_r^*)_{GI}\)

Fstar_1_G1 = Fstar_1_G1_R + Fstar_1_G1_I
Fstar_1_G1.subs({N_w_A1.dt(N).subs(soldict).dot(A1.z): alpha__A1}).subs({-C_51: -C51, -C_61: -C61}).simplify()
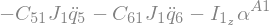
../_images/rocket-car_80_0.png 
Fstar_2_G1 = Fstar_2_G1_R + Fstar_2_G1_I
Fstar_2_G1.subs({N_w_A1.dt(N).subs(soldict).dot(A1.z): alpha__A1}).subs({-C_52: -C52, -C_62: -C62}).simplify()
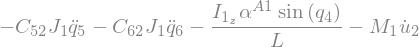
../_images/rocket-car_81_0.png

Gyrostat \(G_2\)

\(\rightarrow {F_G}^* = -m_G {a^G}^*\)

Fstar_G2 = -M2 * N_a_C
Fstar_G2
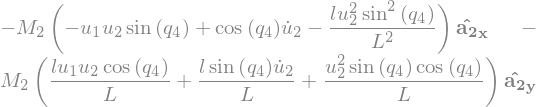
../_images/rocket-car_82_0.png

\(\rightarrow {T_G}^* \overset{\Delta}{=} -[\alpha_A \cdot I_G + {\omega_r}^A \times (I_G \cdot {\omega_r}^A)]\)

Tstar_G2 = -(N_aa_A2.dot(I2) + me.cross(N_w_A2, I2.dot(N_w_A2)))
Tstar_G2
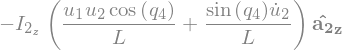
../_images/rocket-car_83_0.png

\(\rightarrow ({F_r}^*)_{GR} = {V_r}^G \cdot {F_G}^* + {\omega_r}^A \cdot {T_G}^*\)

Fstar_1_G2_R = V_1_C.dot(Fstar_G2) + w_1_A2.dot(Tstar_G2).subs(soldict)
Fstar_1_G2_R.subs({N_w_A2.dt(N).subs(soldict).dot(A2.z): alpha__A2})
../_images/rocket-car_84_0.png 
Fstar_2_G2_R = V_2_C.dot(Fstar_G2) + w_2_A1.dot(Tstar_G2).subs(soldict)
Fstar_2_G2_R.subs({N_w_A2.dt(N).subs(soldict).dot(A2.z): alpha__A2})
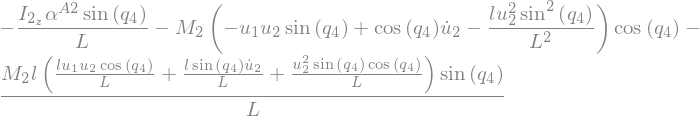
../_images/rocket-car_85_0.png

\(\rightarrow (F_r^*)_{GI} = -J\{\omega_r^A \cdot [\ddot{q_k} g_1 + \dot{q_k} (\omega_3^A g_2 - \omega_2^A g_3)] + C_{kr} (\dot{\omega}_1^A + \ddot{q_k}) \} \qquad (r=1,...,n-m)\)

Here, \(\{\omega_1^A: \omega_2^A,\ \omega_2^A: \omega_3^A,\ \omega_3^A: \omega_1^A\}\)

\(\rightarrow \dot{q_k} = \sum_{s = 1}^{n - m} C_{ks} u_s + D_k\) (Generalized Speeds)

\(\omega_i^A \overset{\Delta}{=} \omega^A \cdot \hat{g}_i \quad (i = 1, 2, 3)\)

# C_kr
C71, C81 = sm.symbols('C_71, C_81')
C_71 = soldict[q7.diff()].diff(u1)
C_81 = soldict[q8.diff()].diff(u1)
Fstar_1_G2_I = -J2 * (N_w_A2.dot(q7.diff().diff() * A2.y + q7.diff()*(N_w_A2.dot(A2.x)*A2.z - N_w_A2.dot(A2.z)*A2.x)) + C_71 * (N_w_A2.dot(A2.y).diff() + q7.diff().diff())) \
               -J2 * (N_w_A2.dot(q8.diff().diff() * A2.y + q8.diff()*(N_w_A2.dot(A2.x)*A2.z - N_w_A2.dot(A2.z)*A2.x)) + C_81 * (N_w_A2.dot(A2.y).diff() + q8.diff().diff()))   # B1 \ B2

Fstar_1_G2_I, C_71, C_81, # Fstar_1_G2_I.subs({-C_71: -C71, -C_81: -C81}).simplify()
../_images/rocket-car_86_0.png 
# C_kr
C72, C82 = sm.symbols('C_72, C_82')
C_72 = soldict[q7.diff()].diff(u2)
C_82 = soldict[q8.diff()].diff(u2)
Fstar_2_G2_I = -J2 * (N_w_A2.dot(q7.diff().diff() * A2.y + q7.diff()*(N_w_A2.dot(A2.x)*A2.z - N_w_A2.dot(A2.z)*A2.x)) + C_72 * (N_w_A2.dot(A2.y).diff() + q7.diff().diff())) \
               -J2 * (N_w_A2.dot(q8.diff().diff() * A2.y + q8.diff()*(N_w_A2.dot(A2.x)*A2.z - N_w_A2.dot(A2.z)*A2.x)) + C_82 * (N_w_A2.dot(A2.y).diff() + q8.diff().diff()))   # B1 \ B2

display(Fstar_2_G2_I)
display(C_72)
display(C_82)
display(Fstar_2_G2_I.subs({-C_72: -C72, -C_82: -C82}).simplify())
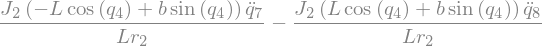
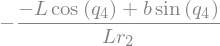
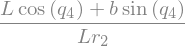
../_images/rocket-car_87_0.png ../_images/rocket-car_87_1.png ../_images/rocket-car_87_2.png ../_images/rocket-car_87_3.png

\(\rightarrow (F_r^*)_G = (F_r^*)_{GR} + (F_r^*)_{GI}\)

Fstar_1_G2 = Fstar_1_G2_R + Fstar_1_G2_I
# Fstar_1_G2.subs({N_w_A2.dt(N).subs(soldict).dot(A2.z): alpha__A2}) # .subs({-C_71: -C71, -C_81: -C81}).simplify()
Fstar_1_G2 = 0

Here, \(\{a_1^C: a_2^C,\ a_2^C: a_3^C,\ a_3^C: a_1^C\}\)

Fstar_2_G2 = Fstar_2_G2_R + Fstar_2_G2_I
Fstar_2_G2.subs({N_w_A2.dt(N).subs(soldict).dot(A2.z): alpha__A2}).subs({N_v_C.dt(N).subs(soldict).dot(A2.x): a_3__C}).subs({N_v_C.dt(N).subs(soldict).dot(A2.y): a_1__C}).subs({-C_72: -C72, -C_82: -C82}).simplify()
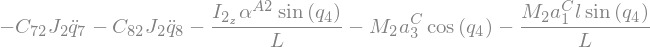
../_images/rocket-car_89_0.png

Variable-Mass Particle, \(P\)

\(\rightarrow {F_G}^* = -m_G {a^G}^*\)

Fstar_P = -m * N_a_P
Fstar_P
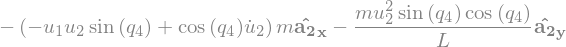
../_images/rocket-car_90_0.png

\(\rightarrow ({F_r}^*)_{GR} = {V_r}^G \cdot {F_G}^*\)

Fstar_1_P_R = V_1_P.dot(Fstar_P)
Fstar_1_P_R
../_images/rocket-car_91_0.png 
Fstar_2_P_R = V_2_P.dot(Fstar_P)
Fstar_2_P_R
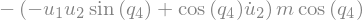
../_images/rocket-car_92_0.png

\(\rightarrow (F_r^*)_G = (F_r^*)_{GR}\)

Fstar_1_P = Fstar_1_P_R
Fstar_1_P
../_images/rocket-car_93_0.png

Here, \(\{a_1^P: a_2^P,\ a_2^P: a_3^P,\ a_3^P: a_1^P\}\)

Fstar_2_P = Fstar_2_P_R
Fstar_2_P.subs({N_v_P.dt(N).subs(soldict).dot(A2.x): a_3__P}).subs({N_v_P.dt(N).subs(soldict).dot(A2.y): a_1__P}).simplify()
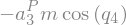
../_images/rocket-car_94_0.png

Generalized Inertia Forces

\(\rightarrow F_r^* = (F_r^*)_{G_1} + (F_r^*)_{G_2} + (F_r^*)_{P} \quad (r = 1, 2)\)

Fstar_1 = Fstar_1_G1 + Fstar_1_G2 + Fstar_1_P
Fstar_1.subs(soldict).simplify()
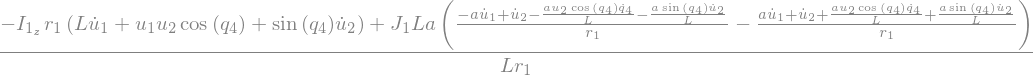
../_images/rocket-car_95_0.png 
Fstar_2 = Fstar_2_G1 + Fstar_2_G2 + Fstar_2_P
Fstar_2.subs(soldict).simplify()
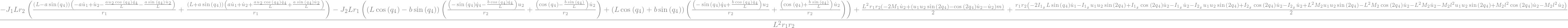
../_images/rocket-car_96_0.png

Velocity of material ejected at \(P\) relative to \(A_2 \rightarrow -C(t)g_3^{'}\)

\(C(t) \rightarrow\) positive

C = me.dynamicsymbols('C')
C_t = -C*A2.x
C_t
../_images/rocket-car_97_0.png

Generalized Thrust

\(\rightarrow F_r^{\prime} \triangleq \sum_{i=1}^{N} \mathbf{V}_{r}^{P i} \cdot \mathbf{C}^{P i} \dot{m}_{i} \quad (r=1, \ldots, k)\)

Fprime_1 = V_1_P.dot(C_t)*m.diff()
Fprime_1
../_images/rocket-car_98_0.png 
Fprime_2 = V_2_P.dot(C_t)*m.diff()
Fprime_2
../_images/rocket-car_99_0.png

Extended Kane’s Equations for Variable-Mass Systems

\(\rightarrow F_r + F_r^* + F_r^{\prime} = 0 \quad (r = 1,..., k)\)

Here, \(F_r = 0 \rightarrow\) no forces contributing to generalized active forces

kane_1 = Fstar_1.simplify() + Fprime_1.simplify()
kane_1.subs(soldict).simplify()
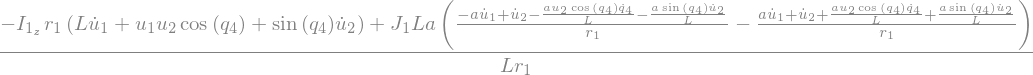
../_images/rocket-car_100_0.png 
kane_2 = Fstar_2 + Fprime_2
kane_2.subs(soldict).simplify()
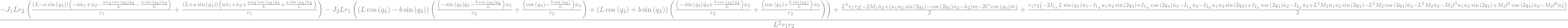
../_images/rocket-car_101_0.png 
kane_1_eq = sm.Eq(kane_1.simplify().subs(soldict).simplify().subs(u).simplify(), 0)
kane_1_eq
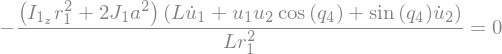
../_images/rocket-car_102_0.png 
kane_2_eq = sm.Eq(kane_2.simplify().subs(soldict).simplify().subs(u).simplify(), 0)
kane_2_eq
../_images/rocket-car_103_0.png

References

Ge1982

Ge, Z., and Cheng, Y. (June 1, 1982). “Extended Kane’s Equations for Nonholonomic Variable Mass System.” ASME. J. Appl. Mech. June 1982; 49(2): 429–431. https://doi.org/10.1115/1.3162105

Kane1978

Kane, T.R., 1978. Nonholonomic multibody systems containing gyrostats. In Dynamics of Multibody Systems (pp. 97-107). Springer, Berlin, Heidelberg.