PyDy’s Documentation¶
PyDy, short for Python Dynamics, is a tool kit written in the Python programming language that utilizes an array of scientific programs to enable the study of multibody dynamics. The goal is to have a modular framework that can provide the user with their desired workflow, including:
Model specification
Equation of motion generation
Simulation
Visualization
Benchmarking
Publication
We started by building the SymPy mechanics package which provides an API for building models and generating the symbolic equations of motion for complex multibody systems. More recently we developed two packages, pydy.codegen and pydy.viz, for simulation and visualization of the models, respectively. This Python package contains these two packages and other tools for working with mathematical models generated from SymPy mechanics. The remaining tools currently used in the PyDy workflow are popular scientific Python packages such as NumPy, SciPy, IPython, Jupyter, ipywidgets, pythreejs, and matplotlib which provide additional code for numerical analyses, simulation, and visualization.
If you make use of PyDy in your work or research, please cite us in your publications or on the web. This citation can be used:
Gilbert Gede, Dale L Peterson, Angadh S Nanjangud, Jason K Moore, and Mont Hubbard, “Constrained Multibody Dynamics With Python: From Symbolic Equation Generation to Publication”, ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2013, 10.1115/DETC2013-13470.
If you have any question about installation, usage, etc, feel free send a message to our public mailing list.
If you think there’s a bug or you would like to request a feature, please open an issue on Github.
Table of Contents¶
Examples¶
Linear mass-spring-damper system with gravity.¶ |
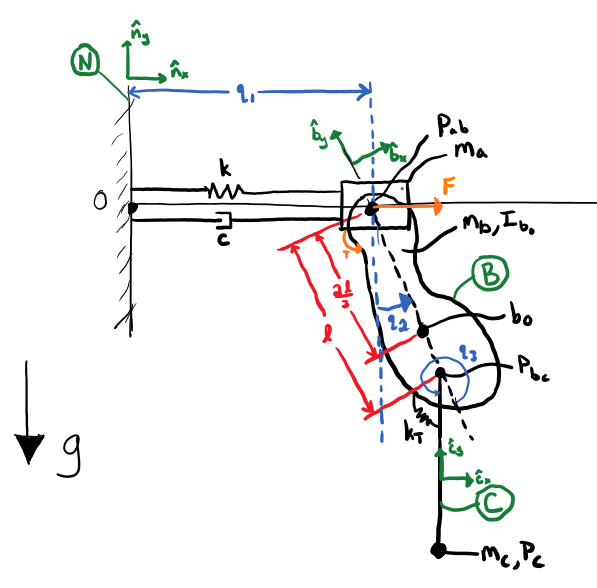
A double compound and simple pendulum.¶ |

Three link conical compound pendulum.¶ |

Carvallo-Whipple bicycle model.¶ |
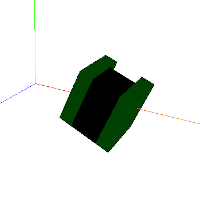
Astrobee free-flying ISS robot.¶ |
3D perpendicular axis double pendulum that exhibits chaos.¶ |

Exercises from Chapter 2 of Kane & Levinson 1985.¶ |

Exercises from Chapter 3 of Kane & Levinson 1985.¶ |
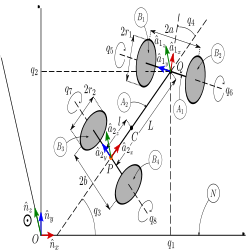
Nonholonomic Rocket Car.¶ |
